Project demo

Tutorial mode

After the intermediate project presentation we changed paths a little bit, although this hasn't really been clear until now. Our original plan was to make a 3D GJK for convex objects and to use it to make a kubb game. However, we were adviced to instead create an interactive GJK tutorial. That is why we have limited our GJK to 2D and instead focused on the concave implementation. 

The first thing we did for our tutorial mode was to show the Minkowski difference.

The Minkowski difference between the shapes S1 and S2 is the set of all points that can be expressed as a point in S1 minus a point in S2. In somewhat mathematical notation, Mdiff = {p1 - p2 : p1 in S1, p2 in S2}. If S1 and S2 are overlapping, there exists a point p that is in both S1 and S2. There fore the point p - p = 0, is in the Minkowski difference. This is the main idea of the GJK algorithm. If the Minkowski difference contains the origin, the shapes are overlapping. 

Of course, we didn't calculate the Minkowski difference by looking at all points in both shapes. We looked at just the Minkowski difference of the set of vertices of each shape, and used Jarvis' gift wrapping algorithm to find the convex hull of the corners found.

😎 😎 😎 😎 😎

The GJK algorithm doesn't look at the entire Minkowski difference to find whether it contains the origin. Instead, it starts with just a line and then adds points to create a subset of the Minkowski difference until it can conclude that it does or cannot contain the origin. Our tutorial mode adds functionality so that the user can step through and visualize each of these steps. 

As can be seen in the above example, if the shape we have right now doesn't contain the origin, we extend the shape in the direction that we think the origin is. We then repeat this until the shape contains the origin, as it will since the shapes are overlapping. In the final step we found that they are indeed overlapping.

When the shapes are not even close to overlapping, the algorithm sometimes only needs one or very few steps to come to this conclusion. This is because we do a check. If we find that we have been searching in the right direction but we are at the end of the Minkowski difference and still haven't found the origin, we can conclude that the Minkowski difference cannot possibly contain the origin.

In the above example, the algorithm terminates after just one iteration.

😎 😎 😎 😎 😎

Now, some of you might have noticed that I wrote that we are using the convex hull to find the Minkowski difference. If we have concave shapes, this won't work correctly. In those cases, we are actually performing GJK multiple times, once for each combination of convex part of the concave shapes. 

In the above example, the left shape has been divided into two convex parts, so there are two Minkowski differences. The idea is the Minkowski difference that we are iterating over right now will be red and the others white, but this isn't really working right now. 

I will now post about a million screenshots to show how GJK works on a concave shape.

The algorithm first looks at the left part of the concave shape (the white Minkowski difference) and correctly concludes that it is not overlapping with rectangle. We then look at the right part.

This Minkowski difference does contain the origin, so we have found that the shapes are overlapping. 

😎 😎 😎 😎 😎

The above examples have been simple enough. Before I finish this extremely long blog post, let's have a look at what happens with a complex concave object that gets divided into many parts.

Clearly, the Minkowski differences are overlapping a lot so there must be a more optimized method than GJK:ing over each one. However, we will not be looking into that for this project. For now, we are viewing this as an educational tool and will simply recommend that the user focuses on simple shapes when in tutorial mode.

Concave shapes integrated

Today we adapted our main algorithm to work with concave shapes. In the previous blog post we divided our concave shapes into convex parts. However, then we GJK'd each of those parts. Now we work on a group of convex pieces as a single unit.

We also made the line work again. We did this by finding the closest distance between all pieces and choosing the shortest one. 

By taking these pictures we also accidentally summoned the devil.

As a bonus, here is one of Rodrigo's artworks:

Concave shapes

One big problem with the GJK algorithm is that it only works for convex shapes. If something is inside the cavity of a concave shape, it will detect an intersection because it is inside the convex hull of the shape.

 

It will also show the closest distance between the shapes as the closest distance to the convex hull.

Since many interesting shapes in applications of collision detection are concave, this is quite limiting. Thankfully, Felix has developed an algorithm which splits a concave shape into convex parts. 

Don't worry about the fact that the lines and the overlapping is a bit chaotic right now. Adapting our GJK algorithm for our new group of convex shapes will be our next step.

Multiple arbitrary shapes

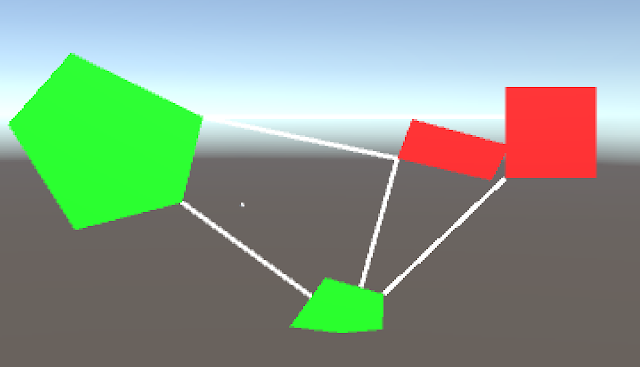
Today we made our application a bit more fun to use. None of us could be bothered to make more test polygons in Blender. Instead, we can now click on arbitrary points in the scene to create a shape that works just like any other polygon.

As you can see, we also added functionality so that lines between all shapes are drawn, and the color changes if a shape intersects with any other.

One problem we have with arbitrary shapes is that our algorithm doesn't work for concave shapes. While Rodrigo and I have been working on the contents of this blog post, Felix has been working on some exciting stuff to fix this but I think that deserves its own blog post because he is a 

😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎😎

Distance between 2D objects

Today we extended our 2D GJK into a version that finds the points on two objects that minimizes the distance between them, as well as calculates that distance. We decided to visualize this new information with a line between the two closest points.

The algorithm works even when the shapes are rotated. When there are several candidates that all give the same distance, only two points are chosen, as can be seen in the first image. When the objects are intersecting, no line is drawn.

We still haven't drawn polygons other than squares to test our algorithm with. However, we tried it with Unity's built in pill shape and we accidentally found out that our algorithm works even for rounded shapes. 

GJK 4 life

First implementation of GJK

Today we implemented a first version of GJK in 2D. For now it only shows us whether or not our 2D shapes are touching. We are planning to extend this version into one which also tells us how far apart they are. We would also like to implement a GJK for 3D.

In our current version, the squares are red when they are touching and green when they are not. The algorithm also works when we rotate the squares.

Although we haven't hard coded the algorithm for squares only, we have only tested it with squares. This is simply because it is the only polygon that is readily available in Unity. Before we move on to our 3D implementation, we will test our algorithm with other polygons.

Setting up the scene

Before we can start implementing GJK we needed to set up the Unity environment we will be working in.

We added a few cubes to a scene and attached a Polygon script which finds all vertices of the shape. Finding the vertices of a shape turned out to be more difficult than expected. There is a built in method called Mesh.vertices which finds all vertices of the mesh. However, it creates duplicates since each corner lies on several different planes. On our cube, for example, each of the six sides has four vertices. Each corner has three vertices with the same position but different normal vectors. Hence, Mesh.vertices gives us a list of 24 vertices. Since we only care about the position, we wanted to remove duplicates. We also had to transform the vectors from coordinates local to the mesh into world coordinates.

In these images you can see that as we move our square, the coordinates (in the bottom right corner of the image) change as well. Our first implementation of GJK will handle 2D objects, so here we have used squares. However, our Polygon script also works on 3D objects, as can be seen below.

The last thing we did today was to create the shell for our GJK script. For now it only finds all Polygons in the scene and adds them to a list. 

Since none of us has much experience working with Unity, this first session was a bit slow and frustrating. Hopefully today's work will enable us to focus on implementing the algorithm.